Spin liquid
In solid-state physics, spin liquid (quantum spin liquid, QSL) denotes a state of matter, where local permanent magnetic moments are present in the material, but do not show any sign of ordering down to the lowest temperatures despite comparable strong antiferromagnetic interactions.[1] Even though many theories study spin liquids, no definite spin-liquid material has been found yet, although there are a few possible spin liquid candidates under investigation.
Contents |
Characteristics of spin liquids
Frustrated magnetic moments
Localized spins are frustrated if there exist competing exchange interactions that can not all be satisfied at the same time leading to a large degeneracy of the system's ground state. A triangle of Ising spins (meaning the only possible orientations of the spins are "up" and "down"), which interact antiferromagnetically, is a simple example for frustration. In the ground state, two of the spins can be antiparallel but the third one can not. This leads to an increase of possible orientations (six in this case) of the spins in the ground state, enhancing fluctuations and thus suppressing magnetic ordering.
Some frustrated materials with different lattice structures and their Curie-Weiss temperature are listed in the table.[1] All of them are proposed spin liquid candidates.
| Material | Lattice | ![\Theta _{cw} [K]](/2012-wikipedia_en_all_nopic_01_2012/I/b83027a986787b24b8b471040d36b087.png) |
|---|---|---|
| κ-(BEDT-TTF)2Cu2(CN)3 | anisotropic triangular | -375 |
| ZnCu3(OH)6Cl2 (herbertsmithite) | Kagomé | -241 |
| BaCu3V2O8(OH)2 (vesignieite) | Kagomé | |
| Na4Ir3O8 | Hyperkagomé | -650 |
| Cu-(1,3-benzenedicarboxylate) | Kagomé | -33 [2] [3] |
| Rb2Cu3SnF12 | Kagomé | [4] |
Resonating valence bonds (RVB)
To build a ground state without magnetic moment, valence bond states can be used, where two electron spins form a spin 0 singlet due to the antiferromagnetic interaction. If every spin in the system is bound like this, the state of the system as a whole has spin 0 too and is non-magnetic. The two spins forming the bond are maximally entangled, while not being entangled with the other spins. If all spins are distributed to certain localized static bonds, this is called a valence bond solid (VBS).
There are two things that still distinguish a VBS from a spin liquid: First, by ordering the bonds in a certain way, the lattice symmetry is usually broken, which is not the case for a spin liquid. Second, this ground state lacks long-range entanglement. To achieve this, quantum mechanical fluctuations of the valence bonds must be allowed, leading to a ground state consisting of a superposition of many different partitionings of spins into valence bonds. If the partitionings are equally distributed, there is no preference for any specific partitioning ("valence bond liquid"). This kind of ground state wavefunction was proposed by P. W. Anderson in 1973 as the ground state of spin liquids[5] and is called a resonating valence bond (RVB) state. These states are of great theoretical interest as they are proposed to play a key role in high-temperature superconductor physics.[6]
Excitations
The valence bonds do not have to be formed by nearest neighbors only and their distributions may vary in different materials. Ground states with large contributions of long range valence bonds have more low-energy spin excitations, as those valence bonds are easier to break up. On breaking, they form two free spins. Other excitations rearrange the valence bonds, leading to low-energy excitations even for short-range bonds. Very special about spin liquids is, that they support exotic excitations, meaning excitations with fractional quantum numbers. A prominent example is the excitation of spinons which are neutral in charge and carry spin 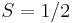 . In spin liquids, a spinon is created if one spin is not paired in a valence bond. It can move by rearranging nearby valence bonds at low energy cost.
. In spin liquids, a spinon is created if one spin is not paired in a valence bond. It can move by rearranging nearby valence bonds at low energy cost.
Identification in Experiments
Since there is no single experimental feature that identifies a material as a spin liquid, several experiments have to be conducted to gain information on different properties which characterize a spin liquid. An indication is given by a large value of the frustration parameter 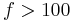 , which is defined as
, which is defined as
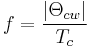
where 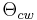 is the Curie-Weiss temperature and
is the Curie-Weiss temperature and 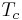 is the temperature below magnetic order begins to develop.
is the temperature below magnetic order begins to develop.
One of the most direct evidence for absence of magnetic ordering give NMR or µSR experiments. If there is a local magnetic field present, the nuclear or muon spin would be affected which can be measured. 1H-NMR measurements [7] on κ-(BEDT-TTF)2Cu2(CN)3 have shown no sign of magnetic ordering down to 32 mK, which is four orders of magnitude smaller than the coupling constant J≈250 K[8] between neighboring spins in this compound. Further investigations include:
- Specific heat measurements give information about the low-energy density of states, which can be compared to theoretical models.
- Thermal transport measurements can determine if excitations are localized or itinerant.
- Neutron scattering gives information about the nature of excitations and correlations (e.g. spinons).
- Reflectance measurements can uncover spinons, which couple via emergent gauge fields to the electromagnetic field, giving rise to a power-law optical conductivity.[9]
References
- ^ a b Leon Balents (2010). "Spin liquids in frustrated magnets". Nature 464 (7286): 199–208. Bibcode 2010Natur.464..199B. doi:10.1038/nature08917.
- ^ A Structurally Perfect S = 1/2 Metal−Organic Hybrid Kagomé Antiferromagnet Emily A. Nytko, Joel S. Helton, Peter Müller, and Daniel G. Nocera J. Am. Chem. Soc., 2008, 130 (10), pp 2922–2923 doi:10.1021/ja709991u
- ^ Phys. Rev. B 80, 132402 (2009) doi:10.1103/PhysRevB.80.132402 Muon-spin spectroscopy of the organometallic spin-1/2 kagome-lattice compound Cu(1,3-benzenedicarboxylate) Lital Marcipar, Oren Ofer, and Amit Keren, Emily A. Nytko, Daniel G. Nocera, Young S. Lee, and Joel S. Helton, Chris Bains
- ^ Pinwheel valence-bond solid and triplet excitations in the two-dimensional deformed kagome lattice K. Matan, T. Ono, Y. Fukumoto, T. J. Sato, J. Yamaura, M. Yano, K. Morita & H. Tanaka Nature Physics 6, 865–869 (2010) doi:10.1038/nphys1761
- ^ P. W. Anderson (1973). "Resonating valence bonds: A new kind of insulator?". Mater. Res. Bull. 8 (2). doi:10.1016/0025-5408(73)90167-0.
- ^ P. W. Anderson (1987). "The resonating valence bond state in La2CuO4 and superconductivity". Science 235 (4793): 1196–1198. Bibcode 1987Sci...235.1196A. doi:10.1126/science.235.4793.1196. PMID 17818979.
- ^ Y. Shimizu, K. Miyagawa, K. Kanoda, M. Maesato, and G. Saito (2003). "Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice". Phys. Rev. Lett. 91 (10). arXiv:cond-mat/0307483. Bibcode 2003PhRvL..91j7001S. doi:10.1103/PhysRevLett.91.107001.
- ^ In literature, the value of J is commonly given in units of temperature (
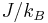 ) instead of energy.
) instead of energy. - ^ T. Ng and P. A. Lee (2007). "Power-Law Conductivity inside the Mott Gap: Application to κ-(BEDT-TTF)2Cu2(CN)3". Phys. Rev. Lett. 99 (15). Bibcode 2007PhRvL..99o6402N. doi:10.1103/PhysRevLett.99.156402.